해시 테이블 (Hash Table)

해시 테이블은 key-value 형식으로 데이터를 저장하는 자료구조로 데이터 탐색 시, 빅-오 O(1)의 성능을 낼 수 있다. 

자료구조 측면에서 해시 테이블, 맵, 사전은 용어의 차이일 뿐 동일하다.

왜 해시 테이블이지? 해시가 뭔데?

해시 테이블은 key를 해시 함수를 거쳐 좁은 범위의 키로 생성하여 테이블에 저장하는 구조이다. 우리가 해시 테이블에서 데이터를 주세요! 라고 던지는게 데이터가 key이고 해시 함수를 거쳐 만들어지는 해시 테이블이 실제 관리하는 key를 해시 값, 이러한 맵핑 과정을 해싱이라고 한다.

해시 테이블의 정의를 다시 말해보면, 해싱된 키와 맵핑되는 데이터를 저장한 자료구조라고 할 수 있다.

 

(출처 - 위키디피아)

수 많은 key들이 해시 함수를 거치면, 동일한 값이 나올 수 있으며, 이를 충돌(collision)이 라고 한다. 아래 글에선 충돌을 해결하기 위한 몇가지 방안들을 소개한다.

열린 어드레스 방법 (Open Addressing method)

1. 선형 조사법

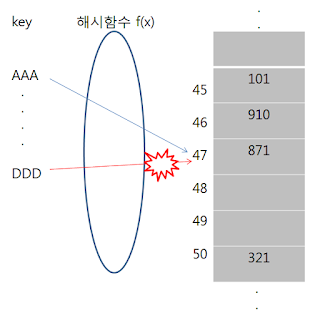
아래 그림에서 key AAA가 해시 테이블에 먼저 데이터를 저장하였고, 뒤 이어 key DDD의 해시 값이 충돌하게 된다. 선형조사법은 바로 옆의 자리가 비었는지 확인 후 비어있으면 그 자리에 데이터를 저장한다. 즉, 그림에선 48 부분에 데이터를 저장한다.

선형 조사법에서 데이터를 찾는 순서는 f(k) + 1 -> f(k) + 2 -> f(k) + 3 -> .... 순으로 진행 된다.

선형 조사법은 클러스터 현상, 즉 특정 영역에 데이터가 몰리는 현상이 발생할 수 있다.

이를 완화 하기위해 충돌 발생 지점에서 먼 곳에서 빈 공간을 찾아보자 라는 아이디어로 이차조사법이 나왔다.

2. 이차 조사법

선형 조사법을 알았다면 이차 조사법은 매우 쉽다. 말 그대로 공간을 좀 더 멀리찾는다. 충돌 발생 시 이차 조사법의 조사 순서는 다음과 같이 전개된다.

f(k) + 1^2 -> f(k) + 2^2 -> f(k) + 3^2 -> ....

3. 이중 해시

이차 조사법은 선형 조사법 보다는 클러스터 현상을 완화시키지만, 해시 값이 같으면 빈 공간을 찾기 위해 접근하는 위치가 항상 동일하다. 이를 해결하기 위해 이중 해시 방법이 나왔다.

이중 해시에서는 두 가지 해시 함수가 존재한다.
첫 번쨰 해시 함수 : key를 해싱하는 과정에서 필요한 해시 함수
두 번쨰 해시 함수 : 충돌이 발생 시 몇 칸 뒤가 비었는지 살피기 위한 함수

이중 해시를 사용할 경우, 키가 다르면 빈 공간을 찾기위해 건너뛰는 길이도 달라 클러스터 현상의 발생 확률을 현저히 낮출 수 있다.

체이닝

체이닝은 닫힌 어드레스 방법으로, 충돌이 발생해도 자신의 자리에 저장하는 방법이다.

즉 동일한 해쉬 값에 대해 여러 값이 저장 될 수 있다.

아래 그림을 보자. AAA는 먼저 해시 테이블에 871이란 데이터를 저장한다. 뒤이어 DDD가 충돌이 발생하는데, 연결리스트를 이용해 동일한 45번 자리에 데이터를 연결시켜 저장한다.